密码子的简并性

“密码子简并”的概念在中学生物里就提过，即几个不同的密码子可以编码相同的氨基酸。但是密码子简并的规律之前却一直是模模糊糊的，趁这次刚完成类似的课题。趁热打铁总结一下：

首先，为了直观、方便地看密码子的简并，我们需要一张“环形密码子图”，而非通常教科书上的那种“方格形密码子表”。下面就是我常用的一张环形密码子图，它的核心由三个同心圆组成：由里到外分别表示第 1 位、第 2 位和第 3 位密码子，外圈是密码子编码的氨基酸及其理化特性。

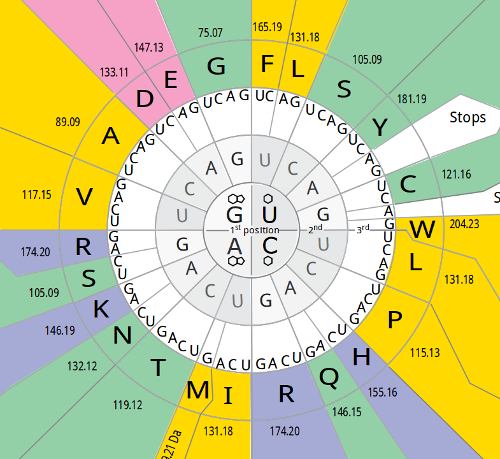
密码子三个位点的简并的规律总结如下：

（一）第 2 位一定不简并。也就是说，任何一个密码子只要第 2 位发生了变化，其编码的氨基酸一定变化。

（二）第 1 位大部分情况下不简并，但有 8 个密码子除外，它们的第 1 位有 1/3 的概率是简并的。例如：AGA 变成 CGA 时氨基酸不变，变成 TGA 或 GGA 时氨基酸变，也就是说：第 1 位随机变化时有 1/3 的概率氨基酸不变。当然，这是假设 A、T、C、G 四种碱基相互转变的概率是一致的前提。这 8 个密码子是：

AGA

AGG

TTA

TTG

CTA

CTG

CGA

CGG

（三）第 3 位的情况就复杂了，分以下几种：

1、第 3 位不简并。该类有 3 个密码子：

ATG

TGA

TGG



例如著名的起始密码子 ATG 编码甲硫氨酸（M），第 3 位碱基 G 变成任意一种其他碱基（A、T、C），氨基酸都会变化（变成异亮氨酸 I）。

2、第 3 位有 1/3 的概率简并。该类有 26 个密码子：

AAA

AAT

AAG

AAC

AGA

AGT

AGG

AGC

TAA

TAT

TAG

TAC

TTA

TTT

TTG

TTC

TGT

TGC

GAA

GAT

GAG

GAC

CAA

CAT

CAG

CAC

3、第 3 位有 2/3 的概率简并。该类只有 3 个密码子：

ATA

ATT

ATC

例如：密码子 ATA 编码异亮氨酸（I），变成 ATT 或 ATC 时仍然编码异亮氨酸（I），而变成 ATG 时则编码甲硫氨酸（M）。

4、第 3 位完全简并。这就是大家常说的“四度简并位点”，该类有 32 个密码子，恰好占密码子总数的一半！

ACA

ACT

ACG

ACC

TCA

TCT

TCG

TCC

GTA

GTT

GTG

GTC

GGA

GGT

GGG

GGC

GCA

GCT

GCG

GCC

CTA

CTT

CTG

CTC

CGA

CGT

CGG

CGC

CCA

CCT

CCG

CCC

因此，总结起来，不同密码子各位点的简并概率是不一样的，笼统地说“第 1，2 位不简并、第 3 位简并”是非常不确切的，必须根据所针对的密码子来确定各位点的简并性。我汇总了一个 Excel 表格大家可以点击下载。（表格中用 0.333 表示 1/3 概率，0.666 表示 2/3 概率）

还有一个有意思的地方是：请注意 CTA 这个密码子，它的第 1 位有 1/3 概率简并，第 3 位则是四度简并位点（概率为 1），那么整个密码子简并的概率难道是 吗？概率超过了 1，显然是不可能的。这是为什么呢？